Dense/Sparse Matrix-Matrix Multiplication
The code written and used for this project can be found here. Details regarding compilation and usage can be found in the README.
Process
I started by defining a way of storing a Sparse Matrix. Many commonly used formats exist including the following:
- Coordinate List (COO) - simple format for dynamic construction of sparse matrices
- Compressed Sparse Row (CSR) - efficient for row-based access, difficult dynamically modifying
- Compressed Sparse Column (CSC) - efficient for column-based access, difficult dynamically modifying
- Dictionary of Keys (DOK) - useful for frequently updated or dynamically constructed matrices
- Block Compressed Row (BCR) - effective when dealing with block-structured sparse matrices, inefficient for matrices with irregular sparsity patterns
- Linked List - educational purposes or simple dynamic updates, high memory overhead
- List of Lists (LIL) - good for incrementally built or modifying sparse matrix, prioritizes ease of element insertion over computational efficiency
Of these, CSR and CSC are the most commonly used due to efficiency in matrix-matrix and matrix-vector operations. Due to the way we learned about matrix storage and multiplication in class, as well as the project description, we have minimal element modification, but plenty of element access and some matrix creation. As such, I settled with Compressed Sparse Row (CSR) Format. CSR Format stores the sparse matrix using 3 arrays:
- Values: Array storing only non-zero elements of the matrix in row-major order (the latter is required for the way we access elements)
- Column Indices: Array storing column indices corresponding to each non-zero value.
- Row Pointers: Array storing the start of each row in the values array
This allows for low memory access overhead due to contiguous data storage and increased efficiency in larger scale arithmetic operations.
We want to analyze the performance differences between multiple cases: dense-dense, dense-sparse, and sparse-sparse, while varying the sparsity with values of 10%, 1%, and 0.1%. Then we want to investigate the effects of different methods of optimization on the efficiency of matrix-matrix multiplication. Specifically, we will be examining the following
- Naive Implementation (no optimization)
- Multi-Threading Only
- SMID Only
- Cache Miss Optimization Only
- Combined Techniques (2-4)
Naive Implementation
The first big issue I ran into was runtime. Although I knew the multiplication would be inefficient, I underestimated how badly it would perform. Despite the original assignment requirements stating that we needed to include matrix multiplication dimensions of 1000x1000 and 10000x10000, at just 5000x5000 I was getting a runtime of 2821.31 seconds (roughly 47 minutes) for 5000x5000 dense-dense multiplication with 10% sparsity. This was unreasonable, but since this is the naive implementation, I could not incorporate any methods of optimization. As such, with the acquiescence of the course instructors, I scaled back the matrix sizes. I ended up with the following data:
Case 3: Sparse-Sparse Multiplication Case 2: Dense-Sparse Multiplication Case 1: Dense-Dense Multiplication
----------- Sparsity 10% ---------- ---------- Sparsity 10% ----------
1000 Time taken: 83 ms 500 Time taken: 121 ms 200 Time taken: 63 ms
2000 Time taken: 604 ms 1000 Time taken: 993 ms 400 Time taken: 626 ms
3000 Time taken: 2033 ms 1500 Time taken: 3382 ms 600 Time taken: 2589 ms
4000 Time taken: 4465 ms 2000 Time taken: 7941 ms 800 Time taken: 8176 ms
5000 Time taken: 8989 ms 2500 Time taken: 15380 ms 1000 Time taken: 16655 ms
6000 Time taken: 14742 ms 3000 Time taken: 27077 ms 1200 Time taken: 31438 ms
7000 Time taken: 23370 ms 1400 Time taken: 57046 ms
8000 Time taken: 34043 ms 1600 Time taken: 93529 ms
9000 Time taken: 47645 ms 1800 Time taken: 135434 ms
10000 Time taken: 66133 ms 2000 Time taken: 192213 ms
---------- Sparsity 1% ---------- ---------- Sparsity 1% ----------
1000 Time taken: 8 ms 500 Time taken: 17 ms
2000 Time taken: 45 ms 1000 Time taken: 117 ms
3000 Time taken: 140 ms 1500 Time taken: 362 ms
4000 Time taken: 292 ms 2000 Time taken: 879 ms
5000 Time taken: 565 ms 2500 Time taken: 1695 ms
6000 Time taken: 847 ms 3000 Time taken: 2784 ms
7000 Time taken: 1300 ms
8000 Time taken: 1825 ms
9000 Time taken: 2367 ms
10000 Time taken: 3126 ms
---------- Sparsity 0.1% ---------- ---------- Sparsity 0.1% ----------
1000 Time taken: 3 ms 500 Time taken: 7 ms
2000 Time taken: 16 ms 1000 Time taken: 30 ms
3000 Time taken: 39 ms 1500 Time taken: 90 ms
4000 Time taken: 63 ms 2000 Time taken: 172 ms
5000 Time taken: 97 ms 2500 Time taken: 296 ms
6000 Time taken: 139 ms 3000 Time taken: 495 ms
7000 Time taken: 193 ms
8000 Time taken: 253 ms
9000 Time taken: 358 ms
10000 Time taken: 418 ms
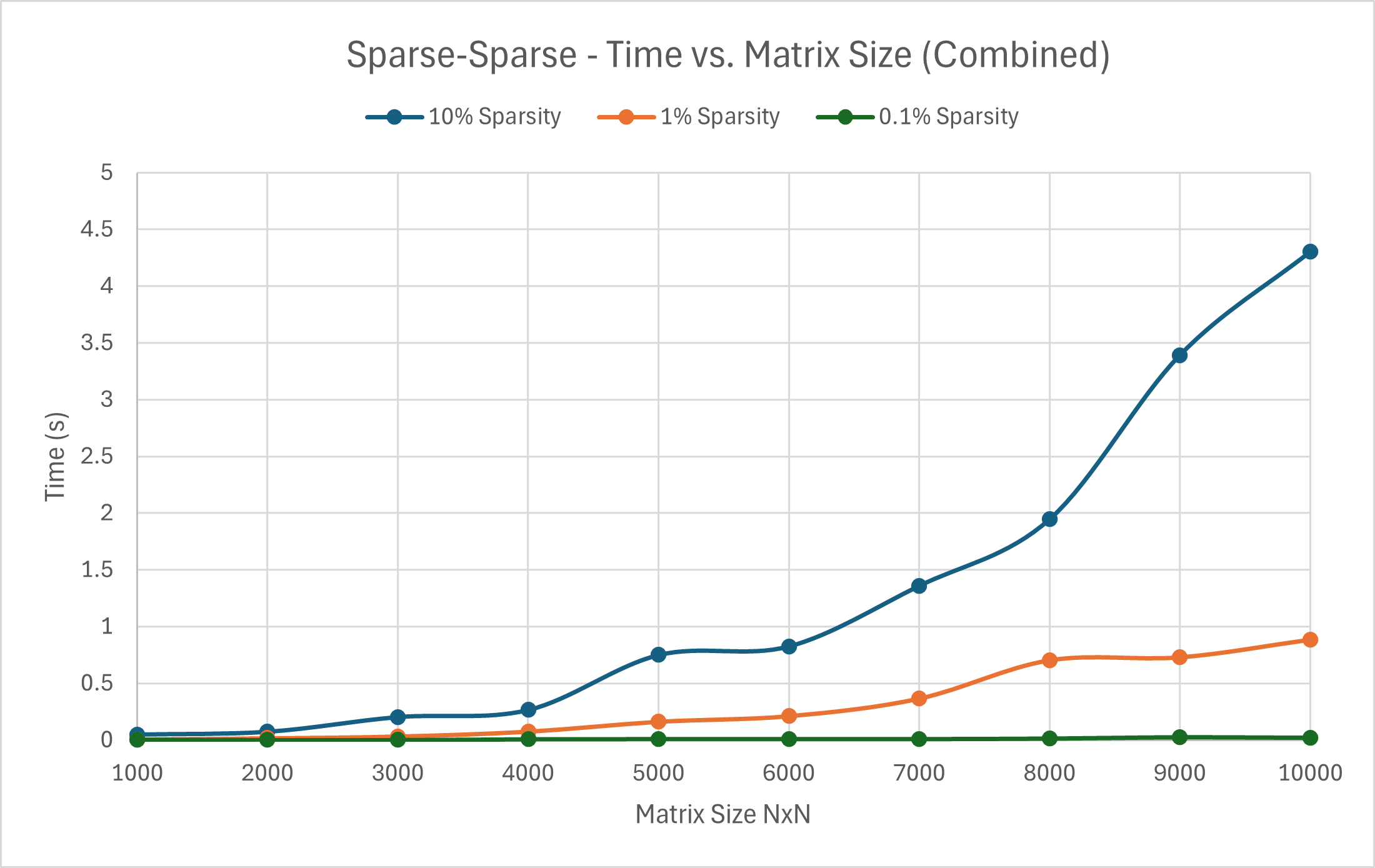
The results can be better visualized in the following graphs. The general trends are as expected. Dense-Dense multiplication takes much longer and scales much faster than Dense-Sparse or Sparse-Sparse, while Dense-Sparse is generally somewhat slower Sparse-Sparse and both appear to scale at a similar rate. We can attribute the variation in Dense-Dense multiplication results to randomization as change in sparsity value has no effect on the former. The effects on sparsity on the runtime are also obvious. The higher the sparsity percentage, the higher the runtime. This can be seen in both the output values above and the graphs below.
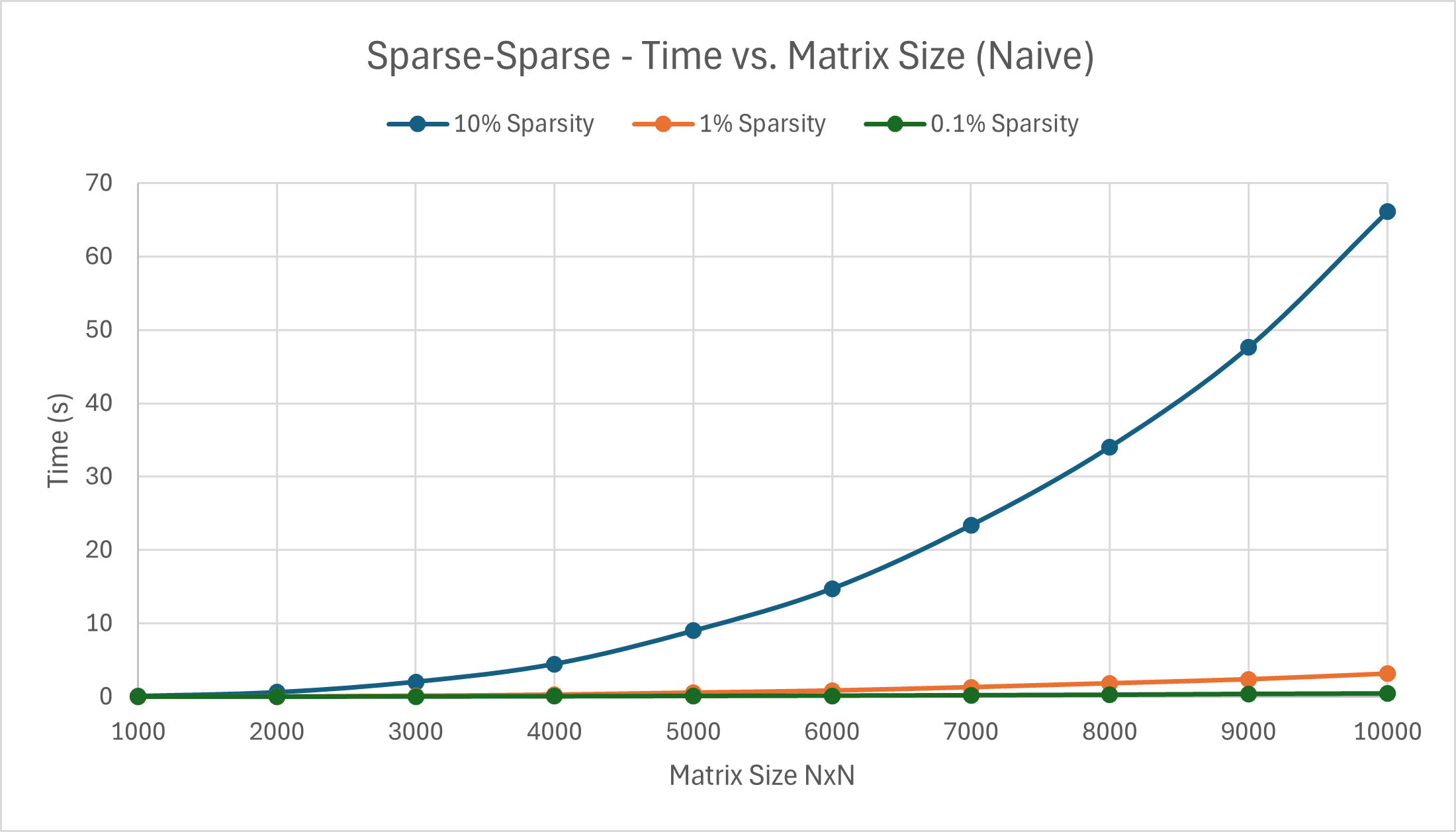
For the sake of time, the results were and will be scaled separately depending on the type of multiplication.
Multi-Threading Implementation
For multi-threading, I know from Project 1 that my computer can handle up to 16 independent threads, so that is the number of threads I had it run.
Case 3: Sparse-Sparse Multiplication Case 2: Dense-Sparse Multiplication Case 1: Dense-Dense Multiplication
---------- Sparsity 10% ---------- ---------- Sparsity 10% ----------
1000 Time taken: 31 ms 500 Time taken: 15 ms 200 Time taken: 12 ms
2000 Time taken: 117 ms 1000 Time taken: 110 ms 400 Time taken: 89 ms
3000 Time taken: 466 ms 1500 Time taken: 384 ms 600 Time taken: 318 ms
4000 Time taken: 836 ms 2000 Time taken: 925 ms 800 Time taken: 730 ms
5000 Time taken: 1438 ms 2500 Time taken: 1715 ms 1000 Time taken: 1682 ms
6000 Time taken: 2407 ms 3000 Time taken: 3214 ms 1200 Time taken: 3045 ms
7000 Time taken: 3619 ms 1400 Time taken: 5666 ms
8000 Time taken: 5285 ms 1600 Time taken: 8426 ms
9000 Time taken: 7765 ms 1800 Time taken: 12709 ms
10000 Time taken: 10630 ms 2000 Time taken: 16828 ms
---------- Sparsity 1% ---------- ---------- Sparsity 1% ----------
1000 Time taken: 4 ms 500 Time taken: 3 ms
2000 Time taken: 14 ms 1000 Time taken: 14 ms
3000 Time taken: 31 ms 1500 Time taken: 52 ms
4000 Time taken: 86 ms 2000 Time taken: 102 ms
5000 Time taken: 153 ms 2500 Time taken: 200 ms
6000 Time taken: 194 ms 3000 Time taken: 322 ms
7000 Time taken: 268 ms
8000 Time taken: 371 ms
9000 Time taken: 545 ms
10000 Time taken: 732 ms
---------- Sparsity 0.1% ---------- ---------- Sparsity 0.1% ----------
1000 Time taken: 2 ms 500 Time taken: 3 ms
2000 Time taken: 4 ms 1000 Time taken: 4 ms
3000 Time taken: 8 ms 1500 Time taken: 12 ms
4000 Time taken: 15 ms 2000 Time taken: 26 ms
5000 Time taken: 18 ms 2500 Time taken: 34 ms
6000 Time taken: 31 ms 3000 Time taken: 51 ms
7000 Time taken: 34 ms
8000 Time taken: 46 ms
9000 Time taken: 57 ms
10000 Time taken: 55 ms
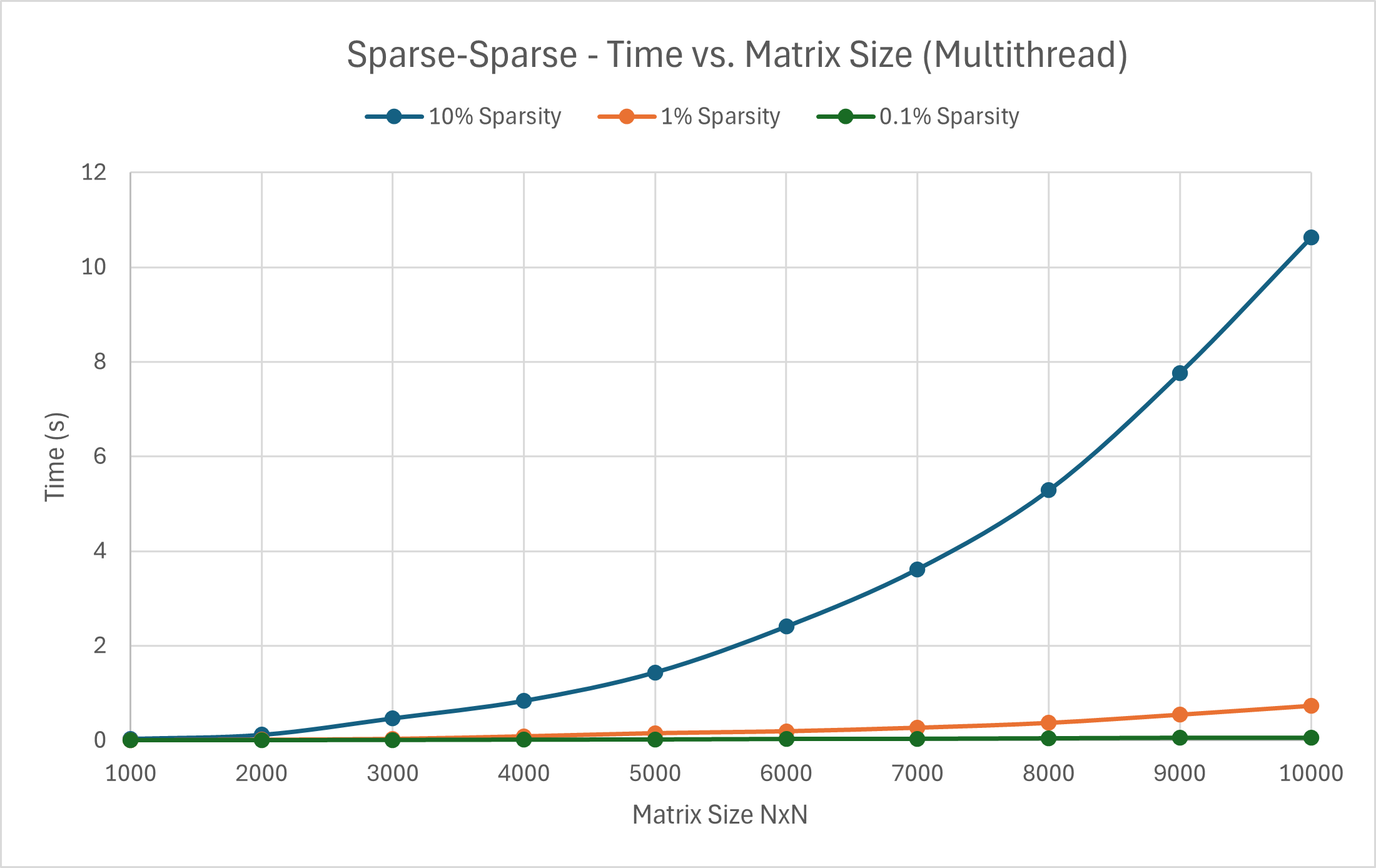
From just the addition of multithreading, the runtime of all forms of multiplication were reduced by roughly an entire order compared to the naive implementation. The difference is notably less for matrices of smaller sizes, where the overhead of creating threads for computation ends up outweighing the actual computation cost. Additionally, it was easy to run into memory allocation issues, so the implementation of the multithreading was a substantial step up in difficulty. ChatGPT also notes that the naive implementation may have better cache locality, especially if implemented in a cache-friendly manner, which we may see more of a difference in later sections.
SIMD Implementation
SIMD (which I frequently mispell as SMID, apologies) stands for “Single Instruction, Multiple Data.” This means applying the same operation to multiple data points in a single CPU instruction, which works well for highly regular operations such as those we use for matrix multiplication. It can also be performed in parallel over small batches of data (e.g. 4 doubles with AVX). It meshes well with multithreading to make the most of your available CPU for operations. However, it is highly dependent on the CPU’s support for vectorized instructions. For example, I ran into quite a bit of error messages when initially compiling my code… This ended up being due to my computer not supporting the default -mavx option for compilation with g++. Instead I had to specify -mavx2 for it properly compile. In older computers, it may not be an option at all, making this the most difficult/complex optimization to implement. All this being said, the performance gain from SIMD optimization should be less than multithreading due to the number of cores my laptop has.
Case 3: Sparse-Sparse Multiplication Case 2: Dense-Sparse Multiplication Case 1: Dense-Dense Multiplication
---------- Sparsity 10% ---------- ---------- Sparsity 10% ----------
1000 Time taken: 0.121089 s 500 Time taken: 0.134503 s 200 Time taken: 0.0129477 s
2000 Time taken: 0.824417 s 1000 Time taken: 1.14332 s 400 Time taken: 0.107831 s
3000 Time taken: 3.04682 s 1500 Time taken: 3.84167 s 600 Time taken: 0.40552 s
4000 Time taken: 7.06708 s 2000 Time taken: 9.73638 s 800 Time taken: 0.999815 s
5000 Time taken: 13.4023 s 2500 Time taken: 18.7687 s 1000 Time taken: 1.99009 s
6000 Time taken: 22.4037 s 3000 Time taken: 30.5019 s 1200 Time taken: 3.52596 s
7000 Time taken: 35.211 s 1400 Time taken: 5.66608 s
8000 Time taken: 53.1216 s 1600 Time taken: 8.54905 s
9000 Time taken: 76.5758 s 1800 Time taken: 12.8665 s
10000 Time taken: 103.705 s 2000 Time taken: 18.6071 s
---------- Sparsity 1% ---------- ---------- Sparsity 1% ----------
1000 Time taken: 0.007506 s 500 Time taken: 0.0171686 s
2000 Time taken: 0.0440724 s 1000 Time taken: 0.13047 s
3000 Time taken: 0.148119 s 1500 Time taken: 0.38692 s
4000 Time taken: 0.398762 s 2000 Time taken: 0.913864 s
5000 Time taken: 0.583384 s 2500 Time taken: 1.83072 s
6000 Time taken: 0.923337 s 3000 Time taken: 3.14378 s
7000 Time taken: 1.39889 s
8000 Time taken: 1.95373 s
9000 Time taken: 2.59043 s
10000 Time taken: 3.33959 s
---------- Sparsity 0.1% ---------- ---------- Sparsity 0.1% ----------
1000 Time taken: 0.00458654 s 500 Time taken: 0.00402979 s
2000 Time taken: 0.0158632 s 1000 Time taken: 0.0223086 s
3000 Time taken: 0.0418012 s 1500 Time taken: 0.0659869 s
4000 Time taken: 0.0621451 s 2000 Time taken: 0.144947 s
5000 Time taken: 0.109877 s 2500 Time taken: 0.26552 s
6000 Time taken: 0.154389 s 3000 Time taken: 0.506078 s
7000 Time taken: 0.207104 s
8000 Time taken: 0.28115 s
9000 Time taken: 0.342577 s
10000 Time taken: 0.442817 s
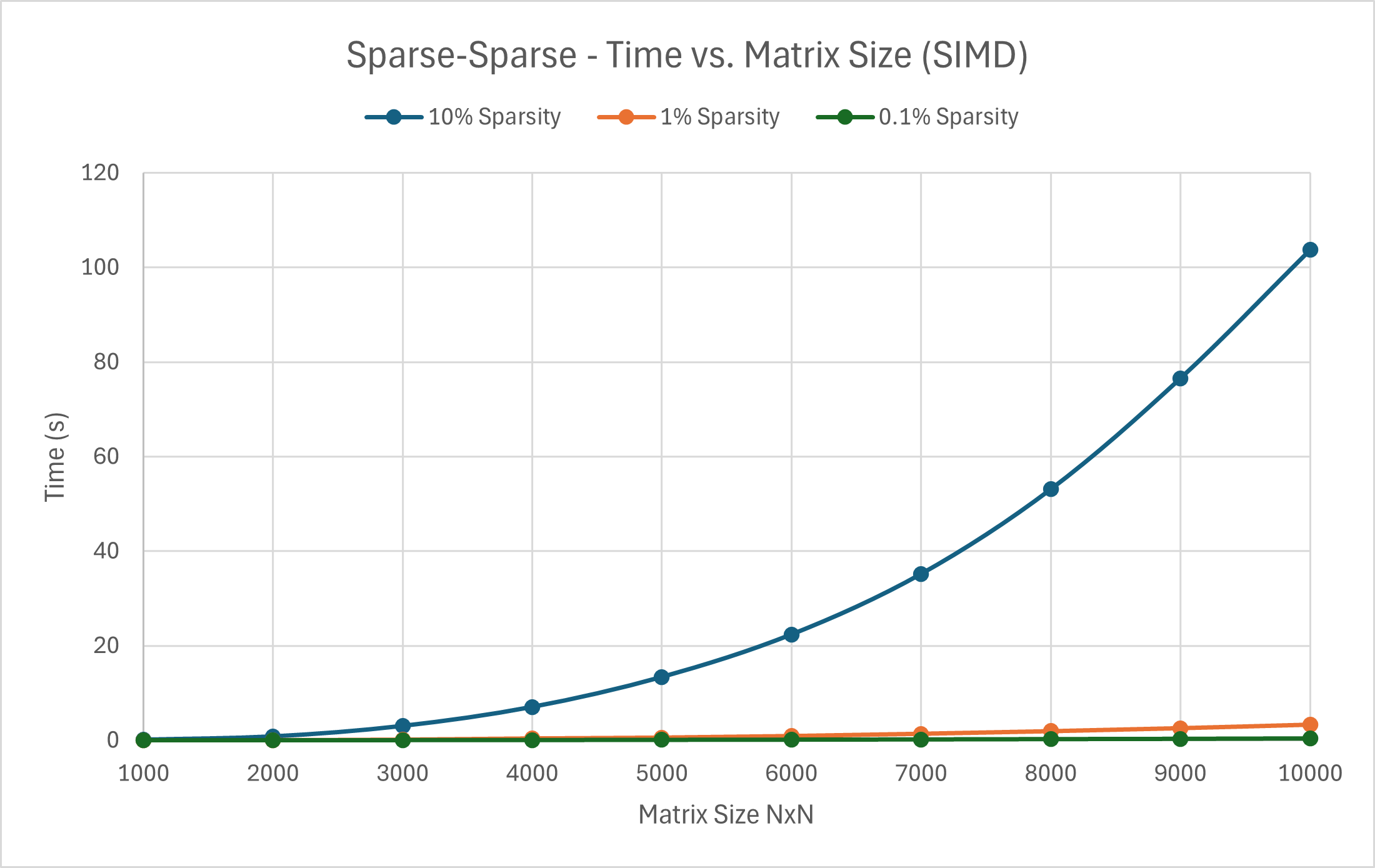
As expected, the results overall are slower than the multithreading approach, but faster than the naive approach. Converse to multithreading, the SIMD implementation does much better for small matrices, which makes sense since we are performing simultaneous operations on 1 CPU core. The combination of both should exponentially improve the performance.
Cache Miss Optimization Implementation
The general concept of cache miss optimization is making most of the existing fast memory access cores available by processing chunks of data that fit in the data cache. By reducing cache misses, we can avoid repeated memory accesses to slower main memory. Loop blocking is a common method of implementation for this, for which I selected a block size of 64. Once more this is largely dependent on the system specs. Information regarding my laptop’s memory specs can be found under Project 1 Results & Analysis.
Case 3: Sparse-Sparse Multiplication Case 2: Dense-Sparse Multiplication Case 1: Dense-Dense Multiplication
---------- Sparsity 10% ---------- ---------- Sparsity 10% ----------
1000 Time taken: 0.12041 s 500 Time taken: 0.113285 s 200 Time taken: 0.0552319 s
2000 Time taken: 0.785189 s 1000 Time taken: 0.981401 s 400 Time taken: 0.478895 s
3000 Time taken: 2.55041 s 1500 Time taken: 3.32997 s 600 Time taken: 1.59336 s
4000 Time taken: 6.11424 s 2000 Time taken: 7.79303 s 800 Time taken: 3.6828 s
5000 Time taken: 10.8446 s 2500 Time taken: 15.2542 s 1000 Time taken: 7.19813 s
6000 Time taken: 18.8116 s 3000 Time taken: 27.5264 s 1200 Time taken: 12.5567 s
7000 Time taken: 29.3523 s 1400 Time taken: 20.0395 s
8000 Time taken: 43.5423 s 1600 Time taken: 29.9193 s
9000 Time taken: 63.2397 s 1800 Time taken: 42.5948 s
10000 Time taken: 84.5609 s 2000 Time taken: 58.8313 s
---------- Sparsity 1% ---------- ---------- Sparsity 1% ----------
1000 Time taken: 0.00440936 s 500 Time taken: 0.0161352 s
2000 Time taken: 0.0355857 s 1000 Time taken: 0.10971 s
3000 Time taken: 0.107994 s 1500 Time taken: 0.352903 s
4000 Time taken: 0.275164 s 2000 Time taken: 0.794612 s
5000 Time taken: 0.523658 s 2500 Time taken: 1.59113 s
6000 Time taken: 0.883524 s 3000 Time taken: 2.8485 s
7000 Time taken: 1.33283 s
8000 Time taken: 2.03297 s
9000 Time taken: 2.81503 s
10000 Time taken: 3.81762 s
---------- Sparsity 0.1% ---------- ---------- Sparsity 0.1% ----------
1000 Time taken: 0.000146468 s 500 Time taken: 0.00312467 s
2000 Time taken: 0.000512253 s 1000 Time taken: 0.0230601 s
3000 Time taken: 0.00178371 s 1500 Time taken: 0.0641407 s
4000 Time taken: 0.00345865 s 2000 Time taken: 0.149822 s
5000 Time taken: 0.00504955 s 2500 Time taken: 0.271734 s
6000 Time taken: 0.00847953 s 3000 Time taken: 0.418494 s
7000 Time taken: 0.015544 s
8000 Time taken: 0.0209704 s
9000 Time taken: 0.031732 s
10000 Time taken: 0.043895 s
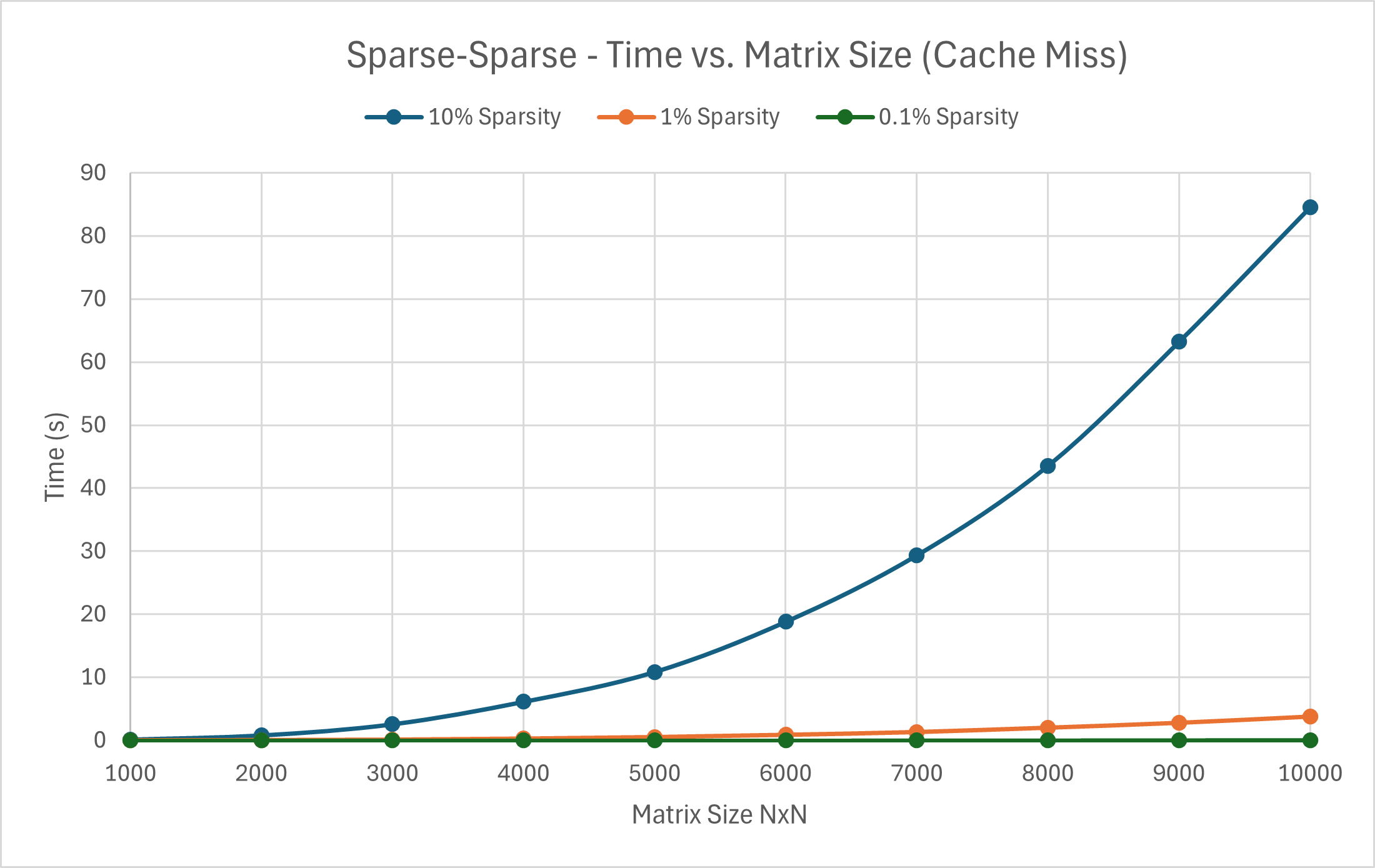
I didn’t have high hopes for this method, but, surprisingly, this was faster than SIMD for all sparsity-related matrix multiplication. Despite being the slowest method for Dense-Dense matrix operations with optimization, it was still a substantial improvement compared to the naive implementation. The lower the sparsity percentage, the closer it came to rivaling the multithreading approach in speed. This difference exemplifies the effects of cache misses and main memory accesses on runtime, as the optimization is intended to. Overall, the less sparse the matrices were, the less the performance gain from this since there were just more baseline memory pulls required.
Combined Implementation
This combination implementation uses loop blocking, SIMD, and multithreading.
Case 3: Sparse-Sparse Multiplication Case 2: Dense-Sparse Multiplication Case 1: Dense-Dense Multiplication
---------- Sparsity 10% ---------- ---------- Sparsity 10% ----------
1000 Time taken: 0.0500951 s 500 Time taken: 0.0115527 s 200 Time taken: 0.00111633 s
2000 Time taken: 0.0751144 s 1000 Time taken: 0.0108954 s 400 Time taken: 0.00894011 s
3000 Time taken: 0.204151 s 1500 Time taken: 0.031387 s 600 Time taken: 0.0142791 s
4000 Time taken: 0.266475 s 2000 Time taken: 0.0689016 s 800 Time taken: 0.0250555 s
5000 Time taken: 0.749967 s 2500 Time taken: 0.136175 s 1000 Time taken: 0.0394458 s
6000 Time taken: 0.826338 s 3000 Time taken: 0.279876 s 1200 Time taken: 0.0873932 s
7000 Time taken: 1.35978 s 1400 Time taken: 0.125216 s
8000 Time taken: 1.9462 s 1600 Time taken: 0.168141 s
9000 Time taken: 3.39149 s 1800 Time taken: 0.225785 s
10000 Time taken: 4.30134 s 2000 Time taken: 0.304109 s
---------- Sparsity 1% ---------- ---------- Sparsity 1% ----------
1000 Time taken: 0.00577733 s 500 Time taken: 0.000586495 s
2000 Time taken: 0.0171185 s 1000 Time taken: 0.0032973 s
3000 Time taken: 0.0329077 s 1500 Time taken: 0.0161029 s
4000 Time taken: 0.0758188 s 2000 Time taken: 0.0203805 s
5000 Time taken: 0.162605 s 2500 Time taken: 0.0329092 s
6000 Time taken: 0.21192 s 3000 Time taken: 0.0469931 s
7000 Time taken: 0.366394 s
8000 Time taken: 0.702776 s
9000 Time taken: 0.72885 s
10000 Time taken: 0.884248 s
---------- Sparsity 0.1% ---------- ---------- Sparsity 0.1% ----------
1000 Time taken: 0.00584964 s 500 Time taken: 0.000515271 s
2000 Time taken: 0.000668794 s 1000 Time taken: 0.00805832 s
3000 Time taken: 0.00130187 s 1500 Time taken: 0.00634668 s
4000 Time taken: 0.00811603 s 2000 Time taken: 0.011154 s
5000 Time taken: 0.00983578 s 2500 Time taken: 0.0233201 s
6000 Time taken: 0.0106066 s 3000 Time taken: 0.0270084 s
7000 Time taken: 0.0104132 s
8000 Time taken: 0.014773 s
9000 Time taken: 0.0260622 s
10000 Time taken: 0.0215956 s
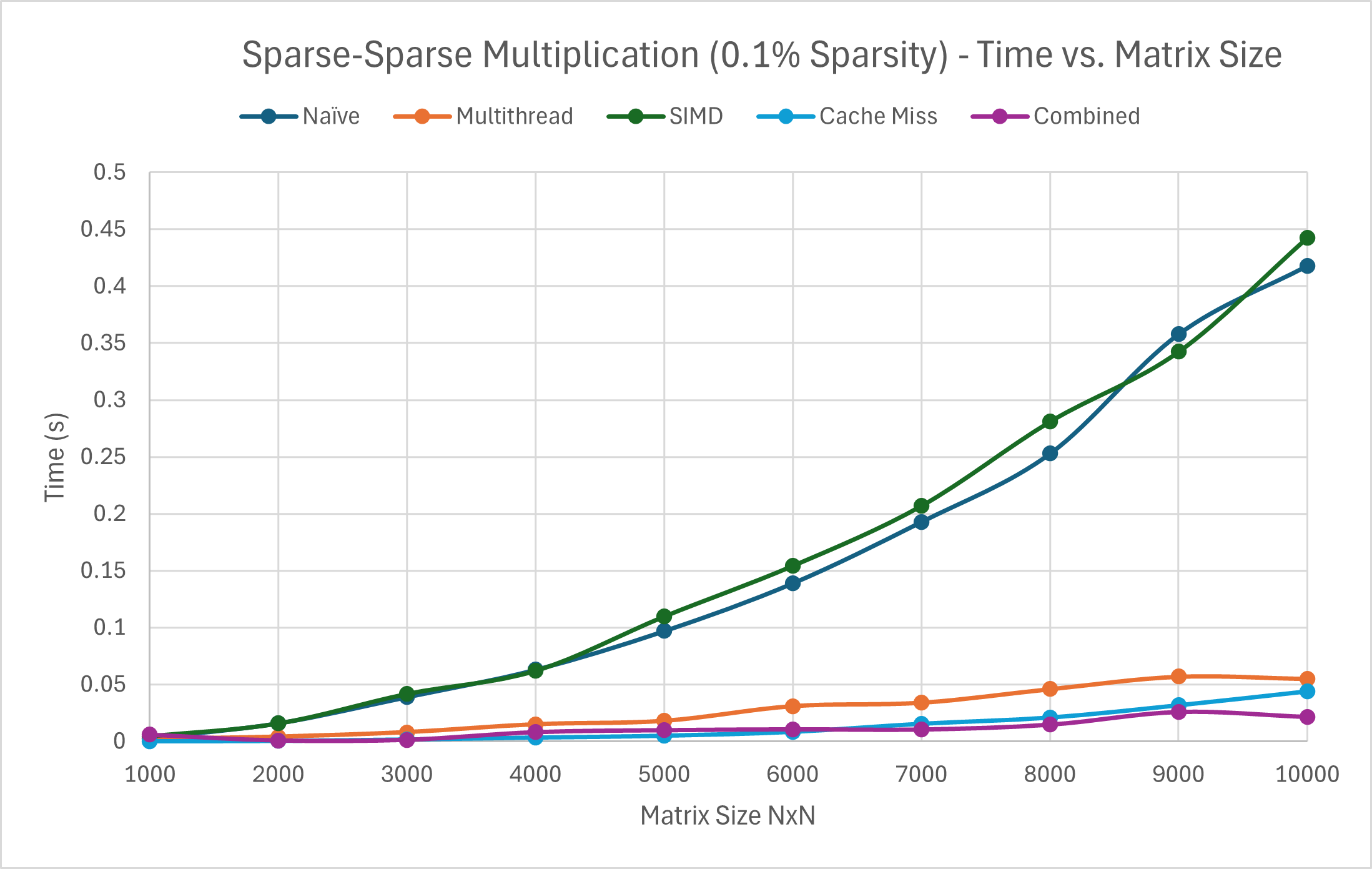
This method had, by far, the best overall performance. Across all results, we can see that the larger the matrix and the higher the percent of non-zero values, the longer the matrix multiplication took. Specifically for this implementation, the improvement is lesser for smaller matrices with more sparsity, likely due to the overhead of multithreading, SIMD, and nested loops.
Method Comparison
For better visualization of the differences and effects of each method and sparsity on performance, the following graphs are provided for reference.
Effects of Optimization on Dense-Dense matrix multiplication
Let us remove the naive implementation’s performance to better see the other methods. 
The naive and cache miss optimization approaches are the worst performing for Dense-Dense matrix multiplication. The difference between the two is, as the method’s name insinuates, due to cache misses (and thus main memory accesses). The gap between cache miss optimization and the other methods is likely due to the parallelism utilized by the other implementations.
Effects of Optimization and Sparcity on Dense-Sparse matrix multiplication
For all dense-dense and dense-sparse matrix multiplication, the combination implementation is generally the best performing, with multithreading following closely in second best. SIMD is generally slower overall likely due to the unfortunately limited parallelization it provides.
Effects of Optimization and Sparcity on Sparse-Sparse matrix multiplication
Citations
ChatGPT used liberally for all parts.